프로그래머를 위한 선형대수 (히라오카 카즈유키 , 호리 겐 지음)
를 바탕으로 공부한 내용을 정리한 포스팅입니다.
선형결합(Linear Combination)
생성(Span)
행렬의 곱셈의 4가지 관점

선형 결합 ( Linear Combinations)
Rn 공간(n은 차원)의 벡터들이 있을때
p개의 가중치 벡터 v1,v2,v3... , p개의 계수 c1,c2,c3....
벡터에 상수배를 해서 더해주는 형식로 선형 결합됨
결과는 같은 n차원

행렬 방정식을 벡터 방정식으로
3개의 방정식으로 이루어진 연립방정식을 행렬을 방정식 하나로 나타낼수 있고
이 행렬 방정식은 벡터 방정식으로 나타낼 수 있음
3개의 방정식은 3개의 세로 재료 벡터가 됨
이렇게 벡터 방정식으로 계산해도 원래 가지고 있던 연립 방정식의 계산과 같음

벡터 방정식은 기하학적 공간상에서의 시각을 제시
이 방정식의 해 존재 유무를 알기 위해서는 span 개념을 알아야함

Span
주어진 재료 벡터를 선형결합 했을 때 가능한 벡터들의 집합을 span이라고 함
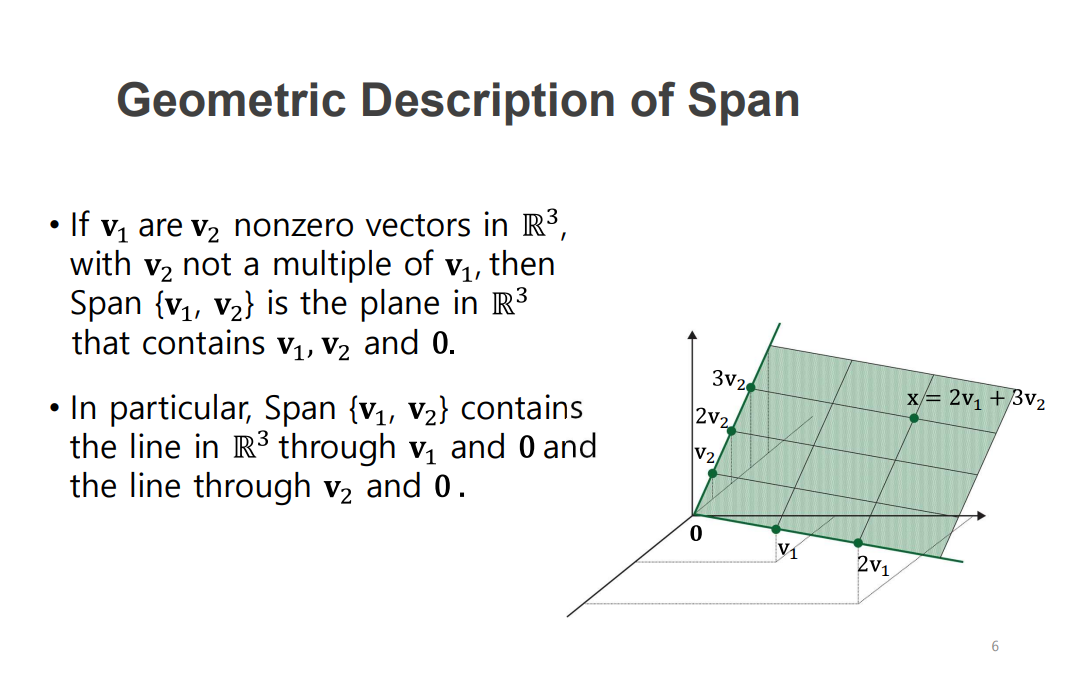
공간상에서의 Span의 개념
두개의 벡터가 있을때
선형결합의 유형
상수배 : 벡터가 가지는 크기와 방향이 있을때 방향은 그대로이면서 크기가 배가됨
두 벡터의 덧샘: 두 벡터가 이룬 평행 사면형의 꼭짓점이 결과가됨
가능한 선형결합의 모든 벡터를 모으면
두 개의 벡터를 사용하여 늘려서 만들 수 있는 평면 위의 모든 점들이 가능한 모든 선형결합의 집합이 됨
- 전체 공간이3차원 공간에서 주어진 유한한 개수의 벡터가 있을때 이 벡터들로 만들 수 있는 선형 결합의 부분 집합 얇은 평면
- 한개가 주어진 경우는 직선이 됨
- 세개의 벡터의 선형결합은 입체 평행사변형 선형결합의 결과
상수배해서 늘이고 줄일 수 있음
3차원 전체를 뒤덮음 전체집합이 이 span과 같음
만약 4차원이라면 3차원 벡터의 선형 조합으로 span으로는 모두 커버할 수 없음
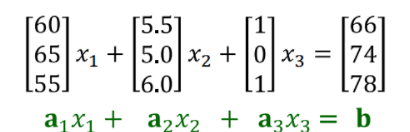
방정식을 푼다는 것 = 이를 만족하는 선형결합의 가중치를 구하는 과정
주어진 3개의 벡터를 길이를 조절하여 꼭지점을 맞추기 위한 비율 : 선혈결합의 가중치
주어진 벡터 방정식으로 봤을때 연립방정식의 근이 존재유무를 span으로 어떻게 알 수 있을까
3개의 재료 벡터와 독립적으로 주어진 또다른 벡터
그 벡터가 3개의 재로 벡터로 만들어지는 Span에 포함이 되어있다면
b 벡터를 3개의 벡터의 선형결합으로 만들 수 있다.
만약 재료 백터가 2개이고 주어진 벡터가 3차원이라면
두개의 선형결합을 가지고 어떤 선형 결합은 표현 불가능
->b 벡터가 앞의 3 벡터의 선형결합으로 나타내어져야함 : 해가 있음
그렇지 않은 경우에는 해가 없음

행렬의 곱을 이해하는 4가지의 시각
행렬곱 = 벡터 간의 선형 조합
행렬곱을 할때
초록 부분을 내적하면 13의 상수값이 나옴
6번을 따로 계산해야함
요소별로 따로 가아니모 한번에 계산할수는 없을까

행렬곱 = 열 벡터 간의 선형 조합
행렬 곱하기 하나의 열 벡터인 경우
왼쪽의 행렬을 3개의 세로 벡터로 사용하고 각 세로 벡터에 가중치를 곱함
행렬 곱하기 여러개의 열 벡터인 경우
3x3 *3x2
결과 행렬의 열벡터을 생각해보면
결과행렬의 첫번째 열벡터는 두번째 행렬의 첫번째 열벡터만 사용함 123
결과 행렬의 두번째 열벡터는 두번째 행렬의 두번째 열벡터만 사용함 -1 0 1
같은 세개의 재료 벡터에 가중치만 달리하여 두개의 결과 벡터가 만들어짐
3개의 재료 열벡터의 선형결합 계수만 달라진 결과
이 두개의 결과 열벡터는 3개 재료 열벡터의 span에 포함됨

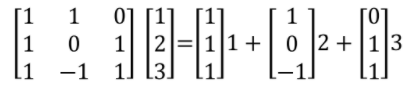
행렬곱 = 행 벡터 간의 선형 조합
AxT를 했을때 결과 행렬도 T버전으로 나오게 됨
같은 3개의 벡터의 선형 결합이지만 1,2,3이 계수가 됨
재료가 오른쪽에서 나오고 행벡터가 재료의 역할을 함

행렬곱 = 외적의 합
내적하고 외적한뒤 커다란 메트릭스 두개를 더하기
많은 머신러닝 문데에서 사용
워드임베딩, pca 에 사용되는 구조

벡터공간에서의 가우시안에서 분산에 해당하는 역할을 하는 공분산 행렬이나 gram 행렬에서도 사용



