비슷한 강의 : 인공지능을 위한 선형대수
[LECTURE] 선형방정식과 선형시스템 : edwith
학습목표 본 강의에서는 선형방정식과 선형시스템의 개념을 구체적인 예시와 함께 배워보겠습니다. 그리고 선형방정식을 풀기 위한 방법 중 한 가지인 역행렬과 항등 행렬의 개념을 배우게...
www.edwith.org
프로그래머를 위한 선형대수 (히라오카 카즈유키 , 호리 겐 지음)
를 바탕으로 공부한 내용을 정리한 포스팅입니다.
- 선형방정식(Linear Equation)과 선형시스템(Linear System)
- 항등 행렬(Identity Matrix)과 역행렬(Inverse Matrix)
- 여러개의 Linear equation을 Matrix계산으로 해결하는 법
1) 선형방정식(Linear Equation)

선형 방정식
선형 방정식은 변수들과 계수들이 주어지고 이 값이 상수와 같다는 형식으로 적을 수 있음
이 식에서 변수를 찾아내는 것이 목표
식은 벡터로 표현 가능
계수를 행 벡터와 변수를 열 벡터로 하고 내적하도록 표현할 수 있음
2) 선형시스템(Linear System)

연립 방정식 = 선형 방정식의 집합
방정식이 여러개 있을때 동시에 만족하는 해를 찾는 것

예를 들어서 기계학습에서 주어진 데이터와 그 데이터의 정답 데이터가 주어졌을때
데이터를 연립 방정식으로 해결할 수 있음
방정식을 출어서 가중치 변수인 x1,x2,x3를 알게되면 새로운 데이터가 입력되었을때 그 데이터의 정답을 맞출 수 있음

직접 연립 방정식으로 해결할 수 있지만 행렬을 사용하여 더 쉽고 편하게 표현가능 함
계수를 모아놓은 행렬 A를 구성
상수를 모아놓은 타겟 값들의 벡터 B
가중치 벡터를 x로 표현

만들어놓은 행렬과 벡터를 사용하여 간단한 식으로 표현할 수 있음
A x = b
행렬의 내적으로 계산하면 연립방정식 계산과 비슷함
내적을 통한 방정식으로 표현 할 수 있음
행렬의 방정식을 선형대수를 통해 어떻게 해결할 수 있을까
-> 역행렬을 사용하여 계산하게 됨
3) 항등 행렬(Identity Matrix)

역행렬을 이해하기 위해서는 항등 행렬이 무엇인지 알아야함
항등행렬:
정사각행렬에서의 가운데의 값은 1이고 남은 값들은 0인 행렬
어떤 행렬과 곱해도 결과는 항상 자기 자신을 만들어냄
4) 역행렬(Inverse Matrix)

항등 행렬을 사용해서 역행렬을 정의할 수 있음
역행렬이란
nxn의 행렬이 있다면 그 해당 행렬의 오른쪽에 곱하거나 왼쪽에 곱했을때 항등 행렬이 나오는 행렬
정사각 행렬만을 대상으로 함
2x2 행렬에서 역행렬을 찾는 공식은 위 사진과 같음

역행렬을 통해서 방정식을 푸는 방법

공식에 행렬을 대입하면 해를 구할 수 있음

최종 해
새로운 데이터가 들어왔을때 저 식에 데이터를 대입하면 수명을 예측할 수 있음

위의 경우는 역행렬이 존재할 때 가능함
일단 역행렬이 존재하게되면 해는 유니크하게 결정됨
역행렬이 있을때 x라는 근은 유니크하게 구할 수 있음 x에 다른 경우를 찾을 수 없음
역행렬이 존재하지 않는 경우는 언제일까
저 식에서 분모가 0인 경우 역행렬이 존재하지 않음
- ad - bc=0 -> ad = bc - > a:b = c:d
- 이 비율의 관계가 만족되면 역행렬이 존재하지 않음
- ad - bc : 역행렬의 존재 유무를 알 수 있는 판별식 determinant of A, det A라고 함
- 3차 이상에서는 다른 식을 사용
- 판별식이 역행렬을 찾을 뿐만아니라 선형변환에서 벡터들의 길이를 얼마나 크게 만들고 작게 만드는지 확대 축소 정도를 determinant의 직관적인 의미도 가지고 있음
-----------------------------------------------------------------------------------------------------------------------------------
<from 프로그래머를 위한 선형대수 >
역행렬 = 역사상
- 정방 행렬 A에 대해 그 역사상에 대응하는 행렬을 A의 역행렬이라고함
- 이동점 을 갖고 원래의 점을 구하는 사상이 A행렬
- 역행렬은 존재할수도 없을수도 있음
- 역행렬이 없는 경우 : 납작하게 눌리는 경우
- 서로 다른 두 점이 A를 적용하면 같은 점으로 이동한다는 의미
- 즉 이동점이 주어져도 원래 x1 였는지 x2 였는지 구별 못함\
- 즉 이동점을 들고 원래의 점 x를 답하는 사상
역행렬의 성질
- 좌표 변환과 행렬
- 좌표 변환은 정방행렬 A를 곱한다라는 형태로 쓸 수 있음 A에는 역행렬이 존재
- 역행렬을 지니는 정방행렬 A를 곱하는 것은 좌표 변환
전치 행렬
- 행렬 A의 행과 열을 바꿔넣는 것
행렬식=부피 확대율
- 면적 확대율에 관한 것을 그 행렬의 행정식(determinant)라고 하고
- det라고 씀
- 3차원 정방행렬이라면 부피 확대율을 의미
- n 차 정발행렬 A에 대해 n차원 판의 부피의 확대율이 행렬식 det A
행렬식의 성질
1) 행렬은 사상
- 행렬식 = 부피 확대율 이라는 관점에서 보면
- det I = 1 #원래 그대로이므로 부피는 1배
- det(AB) = det(A)det(B)
- -> 우선 B에서 부피가 detB배가 되고 그것이 A에서 detA배가 되는 것이므로 B하고 A하면 부피는 det(A)det(B) 배가 됨
- det(A)det(B)=det(AA-1) = det I = 1
- -> 이것은 즉 detA-1 = 1/det A
- det A= 0이면 A-1은 존재하지 않음
2) 행렬식은 어느 열의 정수배를 다른 열에 더해도 값이 변하지 않음
3) 전치 행렬의 행렬식은 원래 행렬의 행렬식과 같음
- 행렬식의 성질은 행과 열의 역할을 모두 바꿔도 성립
----------------------------------------------------------------

2x2행렬이 아닌 더 큰 행렬들의 역행렬은 어떻게 구할까?
더 복잡한 식을 사용, 알고리즘적인 체계적인 과정이 있음

역행렬이 존재하는 경우 해가 유니크 하게 존재
역행렬이 없는 경우 이 판별식을 사용하면 두가지 경우가 나옴
1) 무수히 많은 해
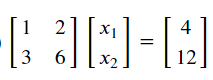
이런 식이 있을 때
x_1 + 2x_2 = 4
3x_1 + 6x_2 = 12
x_1을 소거 하려고 하면 x_2도 0이되고 상수값도 0이됨
두 직선의 방정식에서 해가 유니크 하게 있는 경우 교점이 있지만
이 두식은 직선의 모든 선에서 만남 직선위의 모든 값이 해가 됨
이 두개의 방정식이 동일한 방정식임
-> 해가 무수히 많은 경우
2) 해가 0개
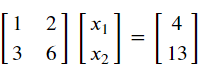
두 직선이 만나지 않으므로 해가 없음

정사각행렬이여야 역행렬을 사용하여 해결할 수 있으나
직사각 행렬에서는 어떻게 해야할까
위의 식에서는 샘플(방정식) 수 m = 변수 n 개 인 mxn 정사각 행렬
- m<n : 변수가 더 많은 경우 해가 무수히 많음 (under determined system)
- m>n : 방정식이 더 많으 경우 -> 해가 없음 (over determined system)
그럼에도 최적의 해를 구할수 있는 방법들이 있을까
정확하게 모든 방정식을 만족할 수는 없지만 가장 근사적으로 해를 찾는 솔루션들이 있음
그 방법들을 이해하기 위한 과정



