활성화 함수에 대해서 공부한 내용을 요약한 글입니다.
활성화 함수의 역할, 종류(Sigmoid. tanh, ReLU)를 공부하고 파이썬으로 구현, 시각화 했습니다.
활성화 함수
입력 신호의 총합을 출력 신호로 변환하는 함수를 일반적으로 활성화 함수라고 합니다.
입력 신호의 총합이 활성화를 일으키는지를 정하는 역할입니다.
아래는 신경망 그림으로 가중치(w)가 달린 입력 신호(x)와 편향(b)의 총합을 계산하고 함수 f에 넣어 출력하는 흐름을 보여줍니다.
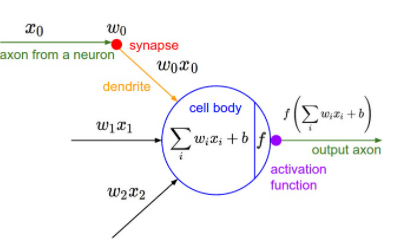
활성화 함수 역할 (비선형 함수여야 하는 이유)
신경망의 활성화 함수는 비선형 함수를 사용해야 합니다.
선형 함수란 출력이 입력의 상수 배만큼 변화는 함수(1개의 곧은 직선)이고
비선형 함수 선형이 아닌 함수로 직선 하나로는 그릴 수 없는 함수입니다.
신경망에서 선형 함수를 이용하면 신경망의 층을 깊게하는 의미가 없어집니다
(활성화 함수를 사용하지 않아도 신경망의 층을 깊게 하는 의미가 없어집니다.)
선형 함수의 문제는 층을 아무리 깇게해도 은닉층이 없는 네트워크로도 똑같은 기능을 할 수 있습니다.
만약 h(x) = cx 를 활성화 함수로 사용한 3층 신경망이 있을 때,
이를 식으로 나타내면 y(x)= h(h(h(x))) 입니다.
이 계산은 y(x)=c*c*c*x 를 수행하지만 사실 y(x)=ax 와 같습니다.
즉 은닉층이 없는 네트워크로 표현 가능한 것입니다.
이처럼 선형 함수인 활성화 함수를 이용하면 여러층으로 구성하는 이점을 살릴 수 없기 때문에
층을 쌓기 위해서는 비선형 함수인 활성화 함수를 사용해야 하고,
활성화 함수로는 비선형 함수를 사용해야 합니다.
활성화 함수로 쓸 수 있는 여러 함수 알아보겠습니다.
1. 시그모이드(sigmoid) 함수

시그모이드(sigmoid)란 'S자 모양'이라는 뜻입니다.
식에서 e 마이너스 x제곱에서 e는 자연 상수로 2.7182... 의 값을 갖는 실수입니다.
실수 값을 입력받아 0~1 사이의 값으로 압축합니다.
큰 음수 값일 수록 0에 가까워지고 큰 양수 값일 수록 1이 됩니다.
오래전에 많이 쓰여왔지만 단점이 몇 가지 있습니다.
단점 1) 기울기 소멸 문제 (Vanishing Gradient Problem)가 발생합니다.
시그모이드 함수의 기울기는 입력이 0일 때 가장 크고, |x| 가 클수록 기울기는 0에 수렴합니다.
이는 역전파 중에 이전의 기울기와 현재 기울기를 곱하면서 점점 기울기가 사라지게 됩니다.
그렇게 되면 신경망의 학습 능력이 제한되는 포화(Saturation)가 발생합니다.
단점 2) 시그모이드 함숫값은 0이 중심 (zero-centered)이 아닙니다.
이러한 경우 학습 속도가 느려집니다.
만약 x가 입력이고 활성화 함수는 sigmoid를 사용하는 신경망을 그림으로 나타내면 아래와 같습니다.

각 노드의 output은 다음과 같습니다.
a1 = w1*h01 + w2*h1
a2 = w1*h11 + w12*h1
a3 = w1*h21 + w22*h1
활성화 함수 적용 후의 output은 h1, h2입니다.
이 신경망의 가중치 기울기를 계산하면 아래와 같습니다.
이때 h21, h22의 값은 시그모이드를 통과한 상태이기 때문에 0~1 사이로 둘 다 양수입니다.
그렇기 때문에 빨간색 글씨의 공통 부분이 양수인 경우에는 기울기 값이 무조건 양수가 되고
빨간색 글씨의 공통 부분이 음수인 경우에는 기울기 값이 무조건 음수가 됩니다.


신경망이 시그모이드를 활성화 함수로 사용했을때 출력으로 가능한 기울기의 부호를 평면 위에 나타낸 그림입니다.
초록 화살표가 최적의 가중치이고 검은 화살표가 최적화를 위한 빠른 길을 의미합니다.

아래 그림에서 가중치가 어떻게 업데이트 되는지를 보여줍니다.
초기화된 가중치에서 업데이트를 시작한다면 w1의 기울기와 w2의 기울기가
둘 다 양수인 경우일직선으로 오른쪽으로 갔다가
둘 다 음수인 경우에는 일직선으로 내려가게 됩니다.
이를 반복하면서 대각선으로 곧장 향하지 못하고 지그재그로 수렴하게 되어 최적화가 오래 걸리는 문제가 있습니다.

3) exp 연산 때문에 자원과 시간이 많이 소모됩니다.
시그모이드 함수 구현하기
시그모이드 함수를 구현하고 그래프를 그려봤습니다.
< Python Code>
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
#그래프 그러보기
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()<결과>

2. tanh 함수

시그모이드와 비슷하지만 실수 값을 입력받아 -1~1 사이의 값으로 압축합니다.
시그모이드를 두배 해주고 -1 한 값과 같습니다.

tanh는 결괏값이 -1~1 사이로 zero-centered 하여 지그재그가 덜하여 시그모이드에 비해 최적화를 잘합니다.
하지만 시그모이드와 같이 기울기 소실 문제를 가지고 있습니다.
tanh 함수 구현하기
tanh 함수를 구현하고 그래프를 그려봤습니다.
< Python Code>
def tanh(x):
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
#그래프 그러보기
x = np.arange(-10.0, 10.0, 0.1)
y = tanh(x)
plt.plot(x, y)
plt.ylim(-1.1, 1.1)
plt.show()<결과>

3. ReLU(Rectified Linear Unit) 함수

가장 많이 사용하는 활성화 함수입니다.
입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 입력을 출력하는 함수입니다.
양수 부분에서는 포화(saturate)가 발생하지 않습니다.
exp 연산이 없어 빠릅니다.
하지만 0 이 중심(zero-centered)이 아니어서 위의 지그재그 문제가 있습니다.
ReLU 함수 구현하기
ReLU 함수를 구현하고 그래프를 그려봤습니다.
< Python Code>
def relu(x):
return np.maximum(0,x)
#그래프 그러보기
x = np.arange(-10, 10)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1, 10.1)
plt.show()<결과>

[출처 & 참고 ]
[1] http://www.cse.iitm.ac.in/~miteshk/CS7015/Slides/Teaching/pdf/Lecture9.pdf
FIG. 3. Commonly used activation functions: (a) Sigmoid, (b) Tanh, (c)...
Download scientific diagram | Commonly used activation functions: (a) Sigmoid, (b) Tanh, (c) ReLU, and (d) LReLU. from publication: Reconstruction of porous media from extremely limited information using conditional generative adversarial networks | Porous
www.researchgate.net
포화(Saturation) 설명
https://m.blog.naver.com/tjdudwo93/221072421443
심층신경망(DNN) in R!!
이번 주제는 머신러닝의 꽃이라 할 수 있는 신경망에 대한 교육자료! 1. 심층신경망(Deep Neural Networ...
blog.naver.com
not zero-centered 설명
Neural Network
Contents Back Propagation Activation Functions Data Preprocessing Weight Initialization Regularizaiton Parameter Optimization Tips to train Neural Network Back Propagation Activation Functions Sigmoid sigmoid 비선형 함수(nonlinearity)는 아래와 같
nmhkahn.github.io
Why are non zero-centered activation functions a problem in backpropagation?
I read here the following: Sigmoid outputs are not zero-centered. This is undesirable since neurons in later layers of processing in a Neural Network (more on this soon) would be receiving ...
stats.stackexchange.com
https://nittaku.tistory.com/267
8. activation function - saturation현상 / zigzag현상 / ReLU의 등장
파이썬 코드로 짠 M.L.N.N.의 코드를 하나하나 살펴보자. 위에는 Multi-Layer Neural Network(fully-connected N.N.)의 prototype이다. 여기서 하나하나의 요소를 개선해서 성능을 높일 수 있다. activation funct..
nittaku.tistory.com
https://sykflyinginthesky.tistory.com/8
Activation Function: Zero-Centered 의 의미 ((Deep) Neural Network)
(Deep) Neural Network 의 Activation Function 들의 특징들을 살펴보다 보면 "Zero-Centered" 라는 개념이 등장한다. 이 페이지에서는 각 activation function 들의 zero-centered 의 여부가 neural network 의 p..
sykflyinginthesky.tistory.com
CS231n Convolutional Neural Networks for Visual Recognition
cs231n.github.io


