비슷한 강의 : 인공지능을 위한 선형대수
를 바탕으로 공부한 내용을 정리한 포스팅입니다.
Least Squares Problem에 대한 소개와 함께 앞으로 Least Squares를 배우는데 필요한 개념들을 배우기
벡터와 관련된 이 개념들은 선형대수에 있어 중요한 개념이니 잘 알아 두기
키워드
내적(Inner Product, Dot Product)
벡터의 길이(Vector Norm)
단위 벡터(Unit Vector)
직교 벡터(Orthogonal Vectors)

Over determinded Linear Systems
방정식의 개수 가 미지수의 개수보다 많은 선형 방정식을 Over determinded Linear Systems라고 합니다.
결정해야 하는 변수는 3개인데 만족해야 하는 방적식이 더 많을 때 determinded에 제약 조건이 많다는 의미입니다.


Over determinded Linear Systems는 해가 없는 경우가 많습니다.
예시처럼 3 변수에 100개의 방정식이 있어서 100차원 차리 벡터가 3개 있는 경우에는 3개의 벡터만으로는 100차원 공간에서 span 했을 때 b가 span안에 포함되기 힘들기 때문입니다.
벡터들이 Span 할 수 있는 공간은 한정되어있지만 방정식이 많아지면 전체 공간이 커지게 되어 해가 없기 쉽습니다.

Leaset Squares 가 필요한 이유
Over determinded Linear Systems는 해가 없지만 근사적으로 해를 구하는 방법을 알아보고 어떻게 근사한 것이 더 좋은 해일지 알아봅니다.
이를 위해 기본적인 개념들을 알아봅니다.

내적( Inner Product)
두 개의 같은 차원을 가지는 벡터가 있을 때, 두 벡터의 내적은 벡터마다 element wise로 곱셈을 해준 뒤 결과를 더하는 것을 의미합니다.
행렬곱으로 나타낼 수도 있습니다. 왼쪽 벡터를 traspose 해서 스칼라 값을 만들어내는 행렬곱 만들 수 있습니다.

내적의 특성
내적은 점으로 표현합니다.
점은 내적이고 점이 없는 경우 행렬 곱을 의미합니다.
a) 교환 법칙 가능
b) 분배 법칙 가능
c) 내적 하고 상수 배 = 상수 배 하고 내적
d) 같은 벡터끼리의 내적은 0보다 크거나 같습니다. 내적이 0인 경우에는 자기 자신이 0인 경우입니다.
예) [x, y]. t [xy]= x2+y2 = 0 인 경우, 이를 위해서는 자기 자신이 0 벡터여야 합니다.
b, c를 사용해서 이러한 식을 만들 수 있습니다.
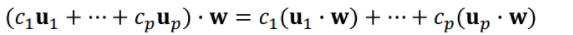
u1부터 up까지 c상수 배 w와 내적 = u, w를 내적 하고 c 상수 배
내적 (변환)이라는 연산은 선형 변환입니다,
내적의 재료로 들어가는 변환들이 내적 하고 설형 결합하나 선형 결함 하고 내적 해도 같습니다.

벡터의 길이 (노름) (vector norm)
직관적 의미로 백터가 주어졌을 때의 길이입니다.
[ 3,4] 가있을 때 [3 제곱, 4 제곱] 루트는 5입니다.
norm (벡터의 길이)은 0보다 크거나 같습니다.
길이를 나타내는 기호는 두 개의 선을 사용합니다.
노름의 제곱은 자기 자신과의 내적을 구한 다음 square root 하는 것과 같습니다.
선행 대수에서 유도하는 과정 중 노름은 내적에 루트로 쓰는 경우가 많습니다.

norm의 기하학적 의미
원래의 벡터 norm에 상수 배 한 값과 상 수배한 벡터의 norm 은 같습니다.
어떠한 벡터(v)와 그 벡터에 상수 배(cv) 했을 때 c ||v|| = ||cv||

단위 벡터 ( Unit vector)
길이가 1인 벡터입니다.
영 벡터가 아닌 어떤 벡터 간의 길이를 1로 만드는 것을 normalizing이라고 하고 이는 벡터의 norm을 구한 뒤 1/||벡터|| 곱합니다.
방향은 바뀌지 않고 길이가 1로 바뀝니다.

두 벡터의 거리 구하기
두 벡터를 빼고 square root를 씌웁니다.
차이 벡터를 구한 다음에 길이를 구하는 norm을 적용하여 두 벡터가 주어졌을 때 거리를 정의한 것입니다.
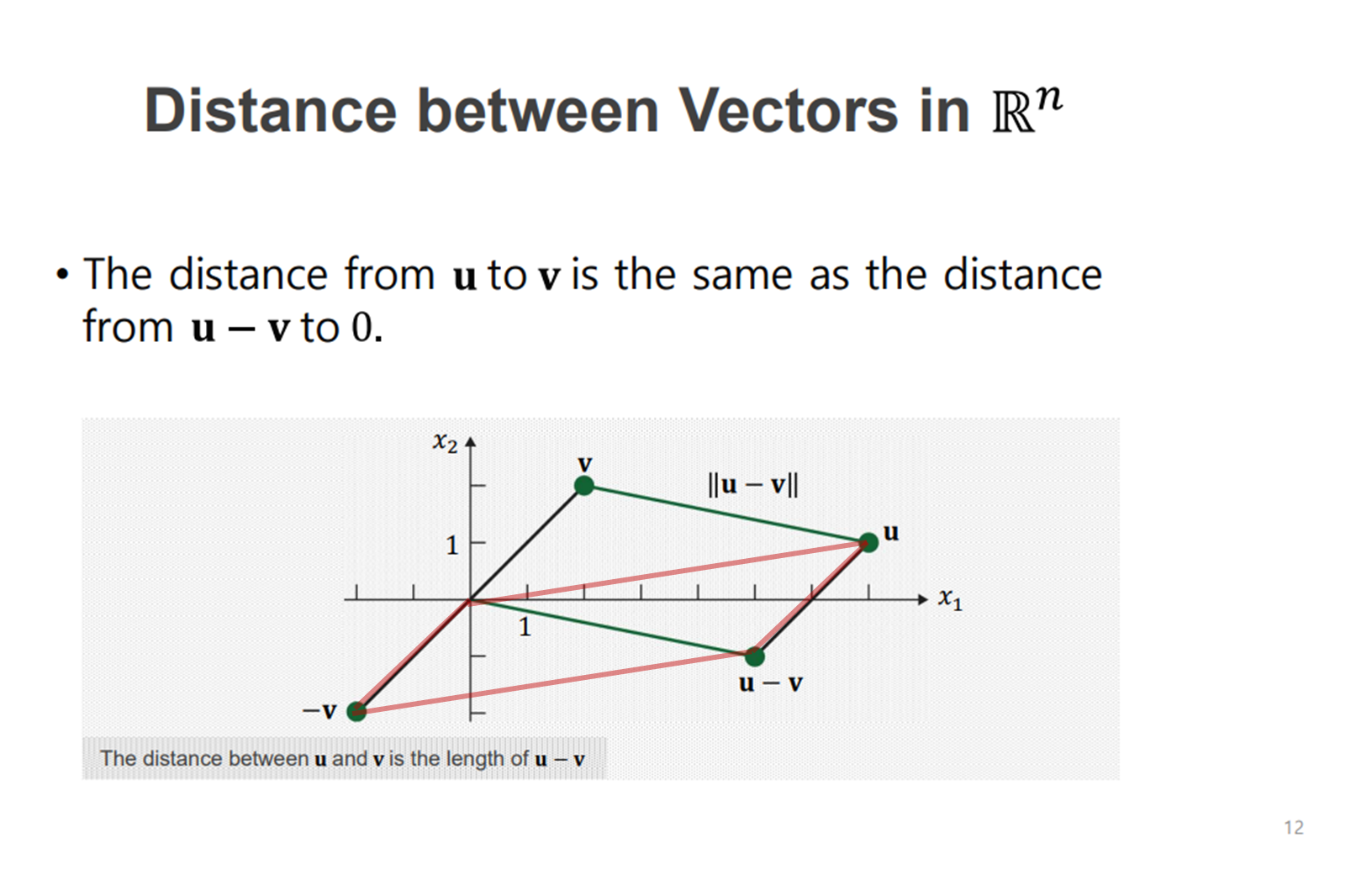
차이 벡터
차이 벡터가가 의미하는 것을 그림으로 보면
u와 v가 주어졌을 때 두 벡터 간의 거리는 u에는 1배 v에는 -1배 해서 나온 벡터의 평행사변형을 통해서 원점에서부터 u-v벡터까지의 길이를 구할 수 있습니다,
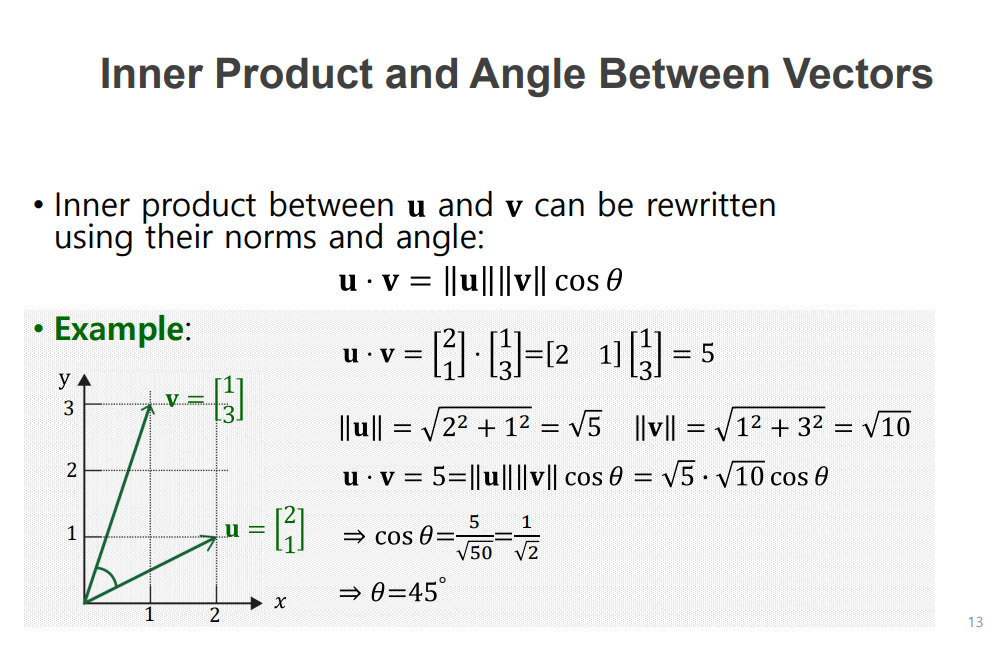
내적으로 두 개의 벡터 각도 구하기
두 개의 벡터의 내적을 구하고 각각 벡터의 길이를 길이 구한 뒤 식에 대입하면 코사인 세타를 구할 수 있습니다.

직교 벡터 ( Orthogonal vectors)
두 벡터가 수직인 경우입니다.
이는 코사인 세타가 90이라는 것이고 두 벡터를 내적 하면 0이 나옵니다.
예) 두 개의 벡터 [2, 3] , [4, -8/3] -> 두 벡터를 내적 하면 0이기 때문에 두 벡터는 수직인 것을 알 수 있음
다시 Over determinded Linear Systems에서 근사적인 해를 구하는 방법을 생각해봅니다.

방정식이 더 많은 Over determinded Linear Systems이 있을 때
우선 이 방정식 3개 만으로 나오는 해를 입력하면 마지막 방정식은 고려를 하지 않은 해이기 때문에 마지막 방정식에 등식을 만족 못합니다.
이때 얼마만큼 그 등식을 만족했는지 정량화하여 Errors를 확인할 수 있습니다.
불완전한 Ax에서 해를 구한 경우 Errors를 구해보면 에 처음 3개의 등식에서는 0 마지막에서는 12가 나옵니다.

다른 새로우 계수 x를 사용해보면 b가 또 다른 값이 나오게 되고 에러를 구했습니다.

두 가지의 계수를 사용하고 Errors를 구해보면 위의 계수와 아래 계수를 사용했을 때 오차가 나는 경향이 다릅니다.
위는 모든 방정식에서 조금씩 에러가 있는 반면 밑에서는 마지막 방정식 하나에서 큰 에러가 있습니다.

sum of squared error
주어진 각각의 학습 데이터마다 모델이 얼마큼 Error를 냈는지 Total Error를 계산할 수 있습니다.
여러 방법이 있지만 sum of squared errors를 많이 사용합니다.
이를 사용해서 정량적인 비교를 보면 위의 솔루션이 더 작은 error를 냈으니 더 좋은 모델이라고 볼 수 있습니다.
이제 더 작은 Error를 최소화하는 방법도 구해야 합니다.

Least Squares Problem
그전에 이 에러를 구하는 방식을 수학적인 목적함수로 만듭니다.
이루고자 하는 목적에 해당하는 함수를 수학적으로 명확하게 정의하는 과정이 첫 번째이고 이를 해결하고자 하는 방법을 찾는 것이 두 번째입니다.
첫 번째를 위한 목적 함수가 위의 식인 Least Squares입니다.
b :실제 주어진 정답 데이터
A : 주어진 변수 , 계수 행렬
x : 구해야 하는 변수 값
일 때
b 벡터에서 Ax를 빼면 error 벡터가 나오고 이 벡터의 길이 ( norm)을 구합니다.
이 에러를 최소화하고 싶기 때문에 앞에 min을 붙여줍니다. 그 밑에는 컨트롤할 수 있는 변수들을 적어주는데 여기서는 x를 적어줍니다.
x를 잘 조절해서 이 값이 최소화되는 최적의 x를 찾는다는 의미로 arg를 사용합니다. 그리고 그 벡터를 x hat으로 사용합니다.



