8 전사함수와 일대일함수 (Onto, One-to-one)

 AI 기술 자연어 처리 전문가 양성 과정 3기 강의

인공지능을 위한 선형대수

를 공부하고 요약한 포스팅입니다.

 

 

 Surjective)
일대일 함수(One-to-one, Injective)
Neural networks에서 전사 함수와 일대일 함수 응용

 

 

<함수 관련 용어 정리>

• 정의역(Domain) :  함수의 입력 변수의 집합 , x가 가능한 전체 집합 
• 공역(Co-domain) : 함수의 출력으로 가능한 집합,  y가 가능한 전체 집합
• 상(image) :  어떤 함수에 대한 정의역의 원소(들) 에 대응하는 공역의 원소(들)
• 치역(range) : 모든 출력값의 집합, 모든 상의 집합 {3,5,7,9} , 

선형 변환에서 나오는 두 가지 개념 

ONTO (전사 함수)

전사 함수란 공역과 치역이 같은 경우를 의미합니다.

공역은 치역의 부분 집합인데
치역이 가장 커질 수 있는 경우가 공역과 치역이 같은 경우입니다.

이는 전체에 사영을 시켰다(전체가 이미지이다) 라는 의미도 됩니다.

필요조건 : 정의역의 수가 공역보다 적어도 같거나 많아야 함(아니면 공역이 존재하게 됨)

오른쪽 그림과 같이  n차원 벡터를 m차원 벡터로 매핑시키는 함수가 ONTO인데,
공역에서 어떠한 점을 뽑아도 거기에 매핑되는 정의역의 원소가 적어도 하나는 있게 됩니다.

n이 입력 벡터(정의역)와
m은 출력 벡터(공역)의 차원 일 때,
3차원(R3) -> 2차원(R2) mapping 은 가능하지만 R2(2차원)-> R3(3차원) mapping은 불가능합니다.
2차원으로는 3차원을 모두 커버할 수 없기 때문입니다.

수학적으로 생각해보면 2차원에서 3차원으로 이동할 때

standard basis vector를 통과시켜서 나온 함숫값을 모아서 Ax 행렬을 만들면

[1, 0] 은 [1, 2, 3]으로 mapping

[0, 1]은 [4, 5, 6]으로 mapping

정의역의 모든 점들은 든 두 개의 벡터로 표현 가능(두 벡터의 선형 결합)

 

 

 

 

 

One -to -one(일대일 함수)

치역이 하나의 정의역에만 대응이 되는 경우를 의미합니다.

2차원(R2)-> 3차원(R3) mapping은 가능하지만
3차원(R3)-> 2차원(R2) mapping 은 불가능합니다. 3차원의 값이 더 많아서 2차원의 값에 하나씩 mapping 할 수 없기 때문입니다. 

 

 

Neural Network의 관점에서 생각해보기

3 가지의 feature인 몸무게 , 키 , 흡연 여부를 사용하여  3차원에서 2차원에서 1차원으로 선형 변환하여 수명을 예측하는 신경망이 있을 때 , 

공역은 1차원(R1)이 되는데 정의역에서 어떤 벡터가 공역으로 mapping 될까요?

one-to-one 이라면 특정한 몸무게 , 특정한 키 , 특정한 흡연 여부를 가지고 있는 한 사람만 78세로 mapping되는 경우이고one-to-one이 아니라면  여러 개의 입력 벡터의 조합들이 78세로 mapping되는 경우입니다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

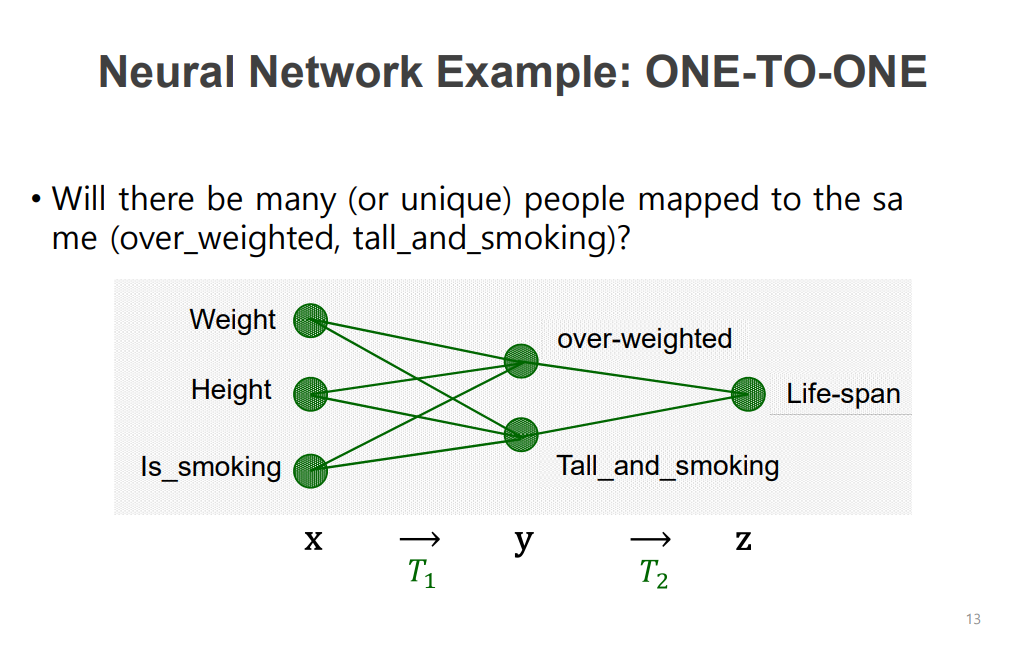
Neural Network에서의 ONE-TO-ONE

각 노드를 만들어내는 선형 결합이 다름(over-weighed선형 결합, Tall_and_smoking 선형 결합)

over weight가 예를 들어 2개의 조합으로 over-weighted = Height - Weight 선형식을 사용할 때

50이 나오는 경우는 다양한 조합이 있음 

몸무게 ,키 ,흡연 유무의 값 자체를 사용하는 것이 아닌 상대적인 차이들을 수명을 예측하는데 의미 있는 값으로 만듦

Neural Network에서의 함수 mapping은 입력이 다양한 벡터이지만
의도적으로 같은 값으로 매핑되어서 수명을 예측하는데 의미 있는 값인 과체중의 정도를 뽑아낼 수 있음

 

 

 

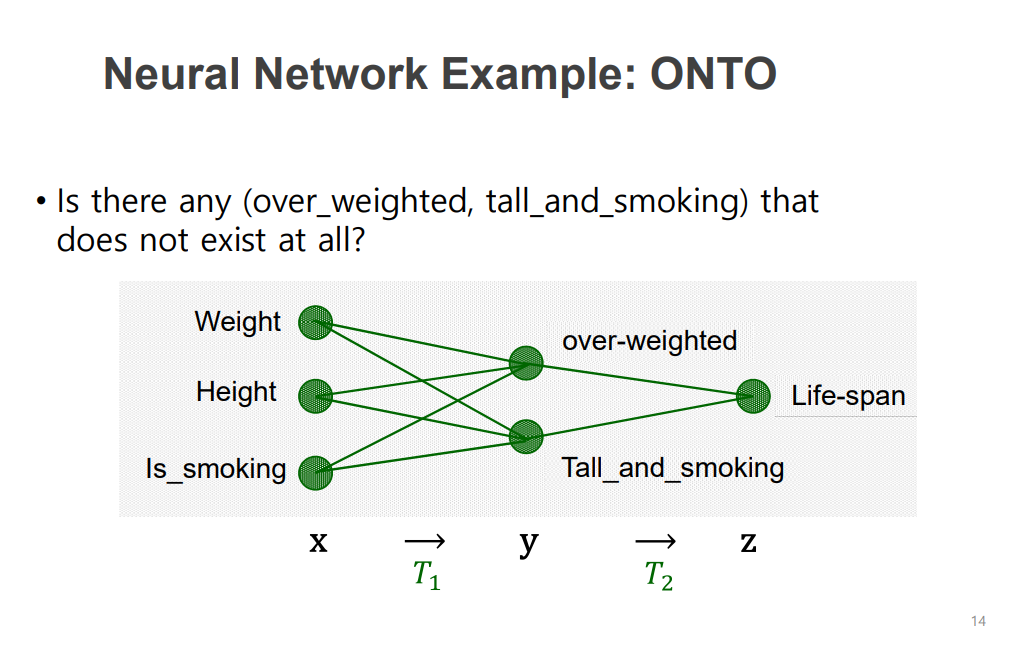
Neural Network에서의 ONTO

입력 노드보다 출력 노드가 많아지는 경우에 사용됨(각 레이어 별로 봤을 때 출력이 더 큰 경우)

GAN, decoding 등에서 사용됨

onto가 될 수도 있지만 어떤 값들에 대한 학습은 못할 수도 있음

 

T가 n차원에서 m차원으로 이동하는 선형 변환일 때  onto인지 one-to-one인지 알아보기

one-to-one : 각 열 벡터가 선형 독립인 경우

on-to : A의 열 벡터들의 span이 Rm이 되는 경우

 

 

 

 

 

 

T가 onto인지 one-to-one인지

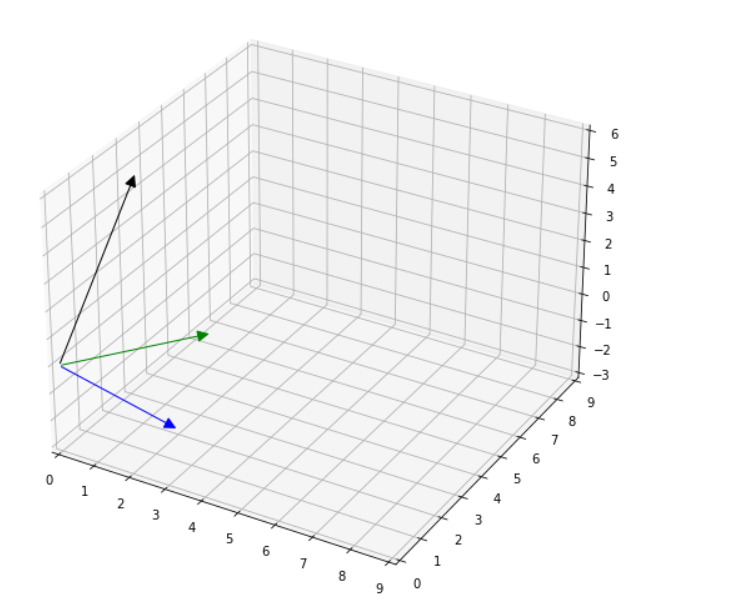
알아보기

T([1,0]) = [2,-1,1 ]이고 T([0, 1]=  [0,1,2] 일 때, 3차원 벡터가 있을 때 

선형  변환이 이러한 관계들을 만족, [1, 0]의 함숫값 [0,1]의 함숫값 Ax의 변환을 정의

one-to-one이라면치역의 원소와 대응하는 x벡터가 하나만 있어야 함  = A의 열이 선형 독립

선형 방정식 관점으로는

해가 여러 개이면 One-to-one이 아닌 Many-to-one

즉 열들이 선형 독립하면 해가 유일해서 one-to-one, 선형 의존하면 해가 무수히 많아서 Many-to-one

위와 같은 경우는 one-to-one이면서 R2는 R2을 매핑할 수 없음

 

T가 onto인지 one-to-one인지 알아보기

[1,2]는 [1,0,0]에 대한 함숫값, [4,3]는 [0,1,0]에 대한 함숫값, [5,6]는 [0,0,1]에 대한 함숫값일 때

R3이 R2로 가는 선형 변환

만약 입력 벡터가 [5 ,6, 7]라면 5[1,2]+6[4,3]+7[5,6]

입력 단에서 저식은 5[1,0,0] 6[0,1,0] 7[0,0,1]으로 조합되기 때문에

각각에 함수값에 해당하는5[1,2]+6[4,3]+7[5,6]에 똑같이 선형 조합해도 똑같다.

그러면 R3이 R2를 모두 커버할까(가능)

3개의 벡터의 span으로 2차원 모두 커버한다-> onto

2차원에서 하나를 뽑았을 대응하는 것이 하나가 아니고 여러 개가 된다.-> one-to-one은 안됨

이 세 개의 벡터가 선형 의존이기 때문에 함숫값 하나에 매핑되는 입력 벡터가 여러 개