6 선형 변환(Linear Transformation)

Goorm : AI 기술 자연어 처리 전문가 양성 과정 3기 강의
인공지능을 위한 선형대수

를 바탕으로 공부한 내용을 요약한 포스팅입니다.

 

<키워드>

선형 변환(Linear Transformation)

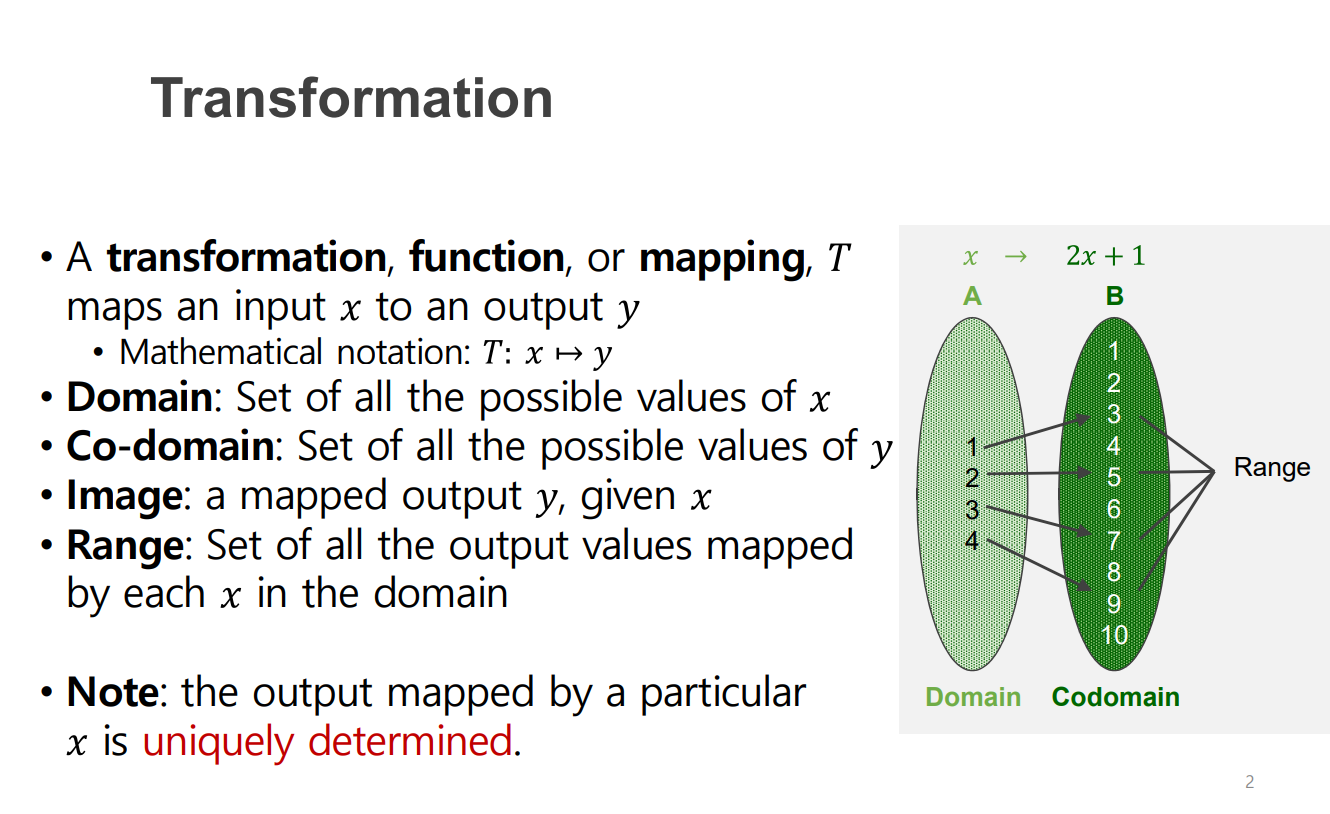
우선 함수의 용어 확인하기

함수 용어

• 정의역(Domain) :  함수의 입력 변수의 집합 , x가 가능한 전체 집합 
• 공역(Co-domain) : 함수의 출력으로 가능한 집합,  y가 가능한 전체 집합
• 상(image) :  1의 상은 3, 2의 상은 5
• 치역(range) : 모든 상의 집합 {3,5,7,9}

 

함수의 조건

• 정의역의 각 원소로부터 공역과 하나씩 연결되어야 함
• 하나의 공역에 여러 개 연결 가능

 

 

 

선형 변환 

정의역과 공역이 벡터 형태의 함수일 때

선형 결합 후 함수에 입력한 함숫값과  각각 입력한 뒤 나온 함숫값에 선형 결합한 값이 같은 경우를 의미

위의 그림과 같이 1을 넣으면 3,  2를 넣으면 6을 이 나오는 함수가 있을 때

(왼쪽의 경우)  4와 5를 사용하여 선형 결합하고 함수에 입력한 값과

(오른쪽의 경우) 1과 2를 입력했을 때 함숫값에서 앞에서 사용한 계수(4,5)로 선형 결합을 했을 때의 값이 같은 경우를 의미

 

 

 

벡터의 변환으로서의 예

정의역이 3차원, 공역이 2차원일 때

상황에 따라서 다른 차원을 가질 수 있음

 

 

벡터에서 벡터의 선형 변환

위의 예시를 보면 두 가지를 알 수 있는데

1) T는 2차원 벡터를 3차원 벡터로 변환시키는 선형 변환

2) T에 [1, 0]을 입력했을 때와  [0, 1]을 입력했을 때의 값을 알 수 있음 

T라는 변환은 무엇일까?

3차원이라는 subspace에서 가장 쉬운 basis는 [0,1,1] ,[ 0, 1, 0], [ 0, 0, 1 ]이고 이때 쓰이는 계수 값으로 이동

입력 벡터를 일단 x1, x2로 정의하고 2차원 standard basis vector 인 [1 ,0], [0 ,1]을 사용하여 선형 결합으로 나타냄

x1, x2를 입력 벡터로 하여 이 두 개의 결합을 먼저 구한 뒤 함수에 입력하거나

함수에 입력한 뒤 나온 결합이 같아야 함

행렬곱의 4가지 관점 중 column벡터 간의 선형 조합을 사용하면 마지막과 같이 쓸 수 있음

 

위에서 선형성 특성과 두 가지 단서를 가지고 T가 저러한 변환이라는 것을 알 수 있었음

어떤 선형성을 만족하는 변환이다 = 항상 행렬과 입력 벡터의  곱으로 나타내어짐

 

 

행렬의 선형 변환

위에서 선형 변환을 알아낸 것을 수식으로 표현하면 입력 벡터에 standard basis vector를 하나씩 넣어봄(en)

basis벡터를 하나씩 입력으로 사용하여 만들어진 출력 벡터들을

columns 순차적으로 쓰면 A 행렬이 됨

=변환에 basis 벡터를 넣었을 때 나온 출력으로 변환을 복원할 수 있음

A는 standard matrix라고 함

 

3차원 벡터에서 2차원 벡터로 선형 변환해주는 예시 

basis 벡터를 넣었을 때 나오는 출력

T라는 행렬에 대한 standard matrix A는

저 basis 벡터 곱들의 출력을 칼럼으로 모아서 A로 구성하면 Ax형태로 나타낼 수 있음